
Optellen t/m 20 via de wisseleigenschap
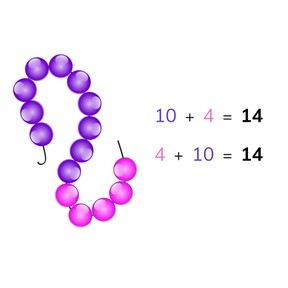


8.000 scholen gebruiken Gynzy
92.000 leerkrachten gebruiken Gynzy
1.600.000 leerlingen gebruiken Gynzy
Algemeen
Leerlingen leren dat het bij een optelsom het niet uitmaakt in welke volgorde de getallen staan, maar dat de uitkomst gelijk blijft.
Belang
Het is handig om dit te weten, omdat de som er soms makkelijker van wordt. Als je het grootste getal vooraan zet, rekent dat vaak makkelijker.
Introductie
Je begint met het splitsen van getallen in de vorm van kralen. Je telt het aantal witte en rode kralen en het totaal. Dit doe je ook met getallen en een splitsdakje. Je kunt er ook nog een aantal mondeling doen, waarbij leerlingen getallen moeten splitsen die jij opnoemt. Bijvoorbeeld: "Het getal 15 splits ik in 4 en in ...". Daarna zorg je dat alle leerlingen (of tweetallen, of per groepje) 20 blokjes hebben. Laat ze het aantal splitsen in twee getallen, bijvoorbeeld in 11 en in 9. Daarbij hebben ze een som gevormd, die uitkomt op 20, namelijk 11 + 9. Schrijf deze som op het bord. Wellicht komen er ook leerlingen op de som 9 + 11. Laat allerlei verschillende splitsingen neerleggen op hun tafel en laat het op het bord zien door de blokjes te verslepen naar elk vak. Schrijf de sommen erbij op het bord. Herhaal dit met een ander splitsgetal. Haal bijvoorbeeld bij elke leerling twee blokjes op, zodat het splitsgetal 18 wordt.
Instructie
Je laat aan de hand van een afbeelding met kralen zien dat als je van een optelsom de getallen omdraait, het antwoord hetzelfde blijft. Je laat hierbij een afbeelding zien met kralen. Vraag hierbij hoeveel kralen je ziet van elke kleur. 4 gele en 9 blauwe. Of 9 blauwe en 4 gele. De sommen die hierbij horen zijn 4 + 9 = 13 en 9 + 4 = 13. De getallen worden omgedraaid, maar de uitkomst is hetzelfde. Herhaal dit meerdere keren met een andere aantallen. Wijs met je vinger bij de kralen die je als eerst optelt en daarna, en andersom. Vraag aan de leerlingen of ze de ene som makkelijker vinden dan de andere som. Sommige leerlingen vinden 15 + 3 makkelijker dan 3 + 15. Daarna laat je een splitsing van het getal 18 zien en de bijbehorende sommen. Dit oefen je samen met de leerlingen met verschillende splitsingen. Na het oefenen met de getallen omdraaien in de som waarbij deze zichtbaar zijn met kralen, leg je uit dat dit ook blijft gelden als je de getallen niet kunt tellen of zien. Oefen samen met de leerlingen zo ook het omdraaien van de getallen en het invullen van de sommen.
Controleer aan de hand van de volgende vragen of leerlingen sommen met de wisseleigenschap beheersen:
- Het getal 16 splits je in 12 en in ...?
- 12 + 4 = 16. Hoeveel is 4 + 12?
- Welke getallen in de som kun je omdraaien?
- Wat gebeurt er met de uitkomst als je de getallen in de som omdraait?
Inoefening
Eerst maken de leerlingen een optelsom met kralen, daarna met splitsdakje en daarna zonder visuele ondersteuning. Ze moeten hierbij steeds de juiste getallen invullen in de sommen.
Afsluiting
Ter afsluiting maak je samen met de leerlingen twee sommen bij de getoonde afbeelding. Daarna doe je hetzelfde, maar met sommen waarbij de splitsing niet zichtbaar is.
Aandachtspunten
Leerlingen die er moeite mee hebben, kunnen de sommen vormen met MAB-materiaal (of rekenrek). Laat ze bijvoorbeeld het getal 18 splitsen in 3 + 15 blokjes. Laat ze het neerleggen en tellen hoeveel dat er samen zijn. Daarna omdraaien, zodat er 15 + 3 blokjes komen te liggen.
Ontdek meer!
Over Gynzy
Gynzy maakt onderwijs makkelijker én leuker. Versterk je onderwijs met kant-en-klare lessen, activiteiten en hulpmiddelen. Hiermee bespaar je tijd die je weer in kunt zetten waar het er echt toe doet: voor de klas.
Gynzy geeft leerkrachten weer tijd om les te geven.



