Cijferend vermenigvuldigen met een getal t/m 1000 en een getal >10

Algemeen

De leerlingen leren cijferend vermenigvuldigen met een getal tot 1000 en een getal groter dan 10.

Belang

Het is belangrijk om cijferend te kunnen vermenigvuldigen, omdat je dan getallen met elkaar kunt vermenigvuldigen die je niet in één keer uit je hoofd kunt uitrekenen.

Introductie

De leerlingen reken de sommen uit. Vraag hoe zij dit gedaan hebben. Hebben zij bijvoorbeeld nullen weggehaald of de som gesplitst?

Instructie

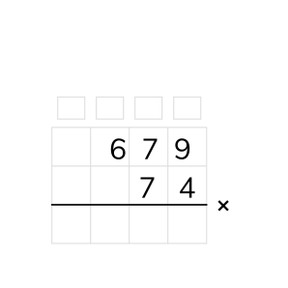
Leg uit dat je bij cijferend vermenigvuldigen begint met het onder elkaar zetten van de getallen. Het grootste getal zet je bovenaan. De D, H, T, E boven de tabel refereren naar de duizendtallen, honderdtallen, tientallen en eenheden. Laat zien dat boven iedere kolom een onthoudhokje staat. In deze onthoudhokjes kun je eventuele overschrijdingen opschrijven om deze later op te tellen bij de andere uitkomsten. De tussenstap in het schema gebruik je om de uitkomsten van het cijferend vermenigvuldigen met de eenheden (E) en met de tientallen (T) op te schrijven. Vervolgens tel je deze twee uitkomsten bij elkaar op voor het antwoord van de som. Leg uit dat je begint met het onderste getal rechts in de kolom van de eenheden (E). Vermenigvuldig dit getal met het bovenste getal uit de kolom van de eenheden (6 × 3 = 18). Van deze 18 schrijf je de 8 op onder de eerste streep in de kolom van de eenheden. De 1 (10) kun je opschrijven in het onthoudhokje van de tientallen. Vermenigvuldig nu het onderste getal uit de kolom van de eenheden met het bovenste getal uit de kolom van de tientallen (6 × 2 = 12). Benadruk dat je niet moet vergeten om de 1 uit het onthoudhokje van de tientallen er bij op te tellen (12 + 1 = 13). Schrijf nu de 3 bij de tientallen (T) en de 1 in het onthoudhokje bij de honderdtallen (H). Vermenigvuldig nu het onderste getal uit de kolom van de eenheden met het bovenste getal uit de kolom van de honderdtallen (6 × 1 = 6). Vergeet niet om de 1 uit het onthoudhokje van de honderdtallen er bij op te tellen (6 + 1 = 7). Dit is de eerste uitkomst van de tussenstap. Vervolgens vermenigvuldig je het onderste getal uit de kolom van de tientallen (T) met het bovenste getal uit de kolom van de eenheden (E) (2 × 3 = 6). Benadruk dat je bij het vermenigvuldigen met een tienvoud eerst een 0 opschrijft in de kolom van de tientallen (T). Vervolgens vermenigvuldig je het onderste getal uit de kolom van de tientallen (T) met het bovenste getal uit de kolom van de tientallen (T) (2 × 2 = 4). Schrijf de 4 op bij de honderdtallen (H) en vermenigvuldig dan het onderste getal uit de kolom van de tientallen (T) met het bovenste getal uit de kolom van de honderdtallen (H) (2 × 1 = 2). Vul de 2 in bij de duizendtallen (D). Benadruk dat dit de tweede uitkomst van de tussenstap is. Als laatste tel je de twee uitkomsten van de tussenstap bij elkaar op (738 + 2460 = 3198). Dit is de uitkomst van de som. Leg uit dat je bij het cijferend vermenigvuldigen met een tienvoud direct een 0 kunt opschrijven bij de eenheden, omdat alle keersommen met dit getal op 0 uitkomen. Laat kort zien dat dit over de sommen 0 × 3, 0 × 2 en 0 × 1 gaat. Oefen samen met de leerlingen twee sommen die via cijferend vermenigvuldigen opgelost moeten worden. Leerlingen kunnen eventueel een kladblaadje gebruiken. De volgende drie sommen maken de leerlingen zelfstandig. Geef vervolgens aan dat er ook sommen zijn met grotere uitkomsten. Leg uit wat de TD en HD in het schema betekenen en laat de leerlingen oefenen met sommen met grotere uitkomsten.

Controleer of de leerlingen cijferend kunnen vermenigvuldigen met een getal tot 1000 en met een getal groter dan 10, door de volgende vraag te stellen:
- Welke stappen gebruik je om de som 209 × 20 cijferend op te lossen?

Inoefening

In de inoefening lossen de leerlingen de opgaven op door cijferend te vermenigvuldigen.

Afsluiting

Bespreek nogmaals het belang van het cijferend kunnen vermenigvuldigen met een getal tot 1000 en een getal groter dan 10. Als afsluiting kun je de leerlingen in tweetallen de som laten oplossen, waarbij ze het antwoord ook weer in appels moeten geven. Om te controleren kunnen de appels naar het schema worden gesleept. Als extra opdracht kunnen de leerlingen zelf een appelsom maken en deze laten oplossen door hun maatje.

Aandachtspunten

Laat leerlingen die moeite hebben met het cijferend vermenigvuldigen met getallen tot 1000, eerst oefenen met cijferend vermenigvuldigen met getallen tot 100. Benadruk dat de leerlingen onthoudhokjes kunnen gebruiken.

Instructiemateriaal

Eventueel een kladblaadje.