
Aftrekken t/m 10.000 via de nulregel
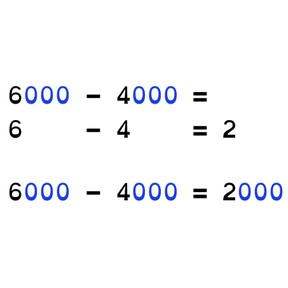


8.000 scholen gebruiken Gynzy
92.000 leerkrachten gebruiken Gynzy
1.600.000 leerlingen gebruiken Gynzy
Algemeen
De leerlingen kunnen aftrekken met duizendvouden t/m met 100 met de nulregel. Ze leren duizendvouden snel af te trekken door gebruik te maken van een hulpsom zonder nullen.
Belang
Als leerlingen aftrekken tot en met 10 000 met de nulregel, kunnen leerlingen veel sneller tienvouden aftrekken.
Introductie
Op het bord staat een bouwwerk met MAB-materiaal met kubussen van 1000 weergegeven. Vraag aan de leerlingen hoeveel blokjes zij denken dat er in het bouwwerk zitten. Je kunt de blokken samen tellen door deze per kubus van 1000 naar de doos te verslepen.
Instructie
Je bespreekt eerst dat heb belangrijk is om met de nulregel te kunnen aftrekken zodat je sneller kunt aftrekken. Bespreek daarna met de leerlingen dat de tienvouden altijd op een nul eindigen, dat de honderdvouden altijd op twee nullen eindigen en dat de duizendvouden op drie nullen eindigen. Dan laat je de nulregel zien met de som 3 - 2 en 30 - 20 en 300 - 200 en 3000 - 2000 met MAB-materiaal, zodat leerlingen een beeld krijgen van de sommen en hulpsommen bij de nulregel.
Vervolgens leg je de nulregel uit met een voorbeeld. Je laat zien dat je bij een som met duizendvouden een hulpsom kunt gebruiken door de nullen weg te halen. Je maakt de som dan duizend keer zo klein. Als je in beide getallen drie nullen hebt, komen er ook drie nullen achter het antwoord van de hulpsom. Leg daarna uit dat als de hulpsom er al staat, je deze kunt gebruiken omdat het antwoord bij elke nul erbij tien keer zo groot wordt en ook een nul erbij krijgt. Oefen vervolgens met drie sommen samen met de leerlingen de nulregel waarbij je steeds vraagt wat de hulpsom is, hoeveel keer zo groot de getallen zijn geworden en wat ze dan met het antwoord moeten doen.
Controleer of de leerlingen kunnen aftrekken met de nulregel tot en met 10.000 met de volgende vragen:
Welke getallen tel je op bij de nulregel?
Wat doe je met duizendvouden als je deze snel wilt aftrekken?
Wat gebeurt er met het antwoord als er nullen bij beide getallen komen?
Inoefening
Je rekent samen met de leerlingen een aftreksom tot en met 10 000 uit waarbij het antwoord al in de hulpsom staat gegeven. Vervolgens werk je samen een aftreksom met duizendvouden uit waarbij het antwoord niet in de hulpsom gegeven staat. Daarna doe je nog een aftreksom met honderdvouden waarbij je terugrekent over de duizend naar een honderdtal.
Afsluiting
Controleer of de leerlingen duizendvouden kunnen aftrekken met de nulregel door te vragen wat je doet met duizendvouden als je deze handig op wilt tellen. Vraag ook waarom het handig is om dit te kunnen en oefen samen nog de som 8000 - 5000. Laat leerlingen daarna in groepjes vier aftreksommen met duizendvouden op kaartjes schrijven en op aparte kaartjes ook de bijbehorende hulpsommen. Laat de leerlingen in groepjes memory spelen met deze kaartjes. Als ze een hulpsom en som hebben gevonden die bij elkaar horen benoemen ze het antwoord.
Aandachtspunten
Leerlingen die moeite hebben met aftrekken t/m 10 000 met de nulregel kun je ondersteunen door met hen samen nog een aantal sommen te oefenen. Je doet dit door zorgvuldig de stappen bij het uitrekenen van een aftreksom t/m 10 000 te doorlopen. Je laat de aftreksom t/m 10 000 zien, maakt samen een hulpsom door de nullen weg te halen en rekent vervolgens de hulpsom en de aftreksom uit. Begin met kleine aftreksommen (zoals 2000 - 1000). Je kunt eerst nog de uitkomst in de hulpsom geven en deze daarna weghalen. Vervolgens oefen je met het aftrekken over het honderdtal (bijvoorbeeld 1200 - 300), en bouw dit uit naar grotere sommen zoals 7000 - 4000.
Instructiemateriaal
lege kaartjes voor memory
Ontdek meer!
Over Gynzy
De digitale oplossingen van Gynzy zijn altijd een waardevolle aanvulling voor jouw basisschool. Versterk je onderwijs met kant-en-klare lessen, activiteiten en hulpmiddelen. Hiermee bespaar je tijd die je weer in kunt zetten waar het er echt toe doet: voor de klas.
Gynzy geeft leerkrachten weer tijd om les te geven.



