
Berekenen van een oppervlakte van een complex figuur


8.000 scholen gebruiken Gynzy
92.000 leerkrachten gebruiken Gynzy
1.600.000 leerlingen gebruiken Gynzy
Algemeen
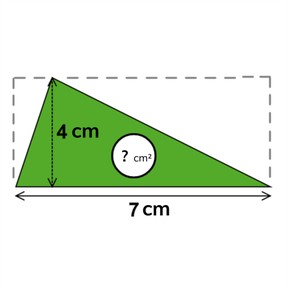
Leerlingen leren de oppervlakte van figuren berekenen. De figuren bestaan uit verschillende soorten driehoeken, parallellogrammen en ruiten.
Belang
Bespreek met de leerlingen dat het handig is om een oppervlakte van verschillende figuren te kunnen berekenen, zodat je weet hoe groot iets is. Bijvoorbeeld als je wilt weten hoe groot het driehoekige vlak van een vlieger is en wat de oppervlakte van de hele vlieger is.
Introductie
Je laat een aantal driehoeken op het digibord zien en vraagt welke oppervlakte bij de figuren horen. Vraag de leerlingen hoe zij dit hebben uitgerekend.
Instructie
Je geeft aan dat je de oppervlakte van een driehoek handig kunt uitrekenen. Je vermenigvuldigt de lengte met de breedte. Het antwoord dat je krijgt geeft de oppervlakte van een rechthoek. Een driehoek is precies de helft van een rechthoek, dus je deelt de uitkomst door 2. Daarna laat je zien hoe je de oppervlakte van een driehoek kunt berekenen door te bespreken hoe je kunt bepalen welke som bij een figuur hoort. Vervolgens bespreek je met de leerlingen een aantal figuren waarbij de leerlingen de oppervlakte berekenen. Ze bedenken eerst welke som ze moeten maken en rekenen deze vervolgens uit. Soms is er een driehoek aan het figuur toegevoegd. De lengtes van de driehoeken tel je bij elkaar op en vervolgens bereken je de oppervlakte van de hele driehoek. Daarna bereken je de oppervlakte van de toegevoegde driehoek. Deze oppervlakte haal je van de uitkomst af. Vervolgens deel je de uitkomst door 2. Ook hierbij bespreek je met de leerlingen hoe zij de oppervlakte berekenen en vervolgens oefenen ze met een aantal figuren. Bespreek dat je bij de oppervlakte van een ruit de diagonalen met elkaar moet vermenigvuldigen. Deze uitkomst deel je door 2. Laat de leerlingen oefenen met een figuur en vraag welke som ze hebben gemaakt. Vervolgens oefenen ze met nog een aantal figuren. Bij een parallellogram kun je een driehoek verplaatsen, waardoor het figuur een rechthoek wordt. Bereken de oppervlakte van de rechthoek. Deze uitkomst is gelijk aan de uitkomst van een parallellogram. Bespreek met de leerlingen welke som je maakt om de oppervlakte van een parallellogram te berekenen en laat de leerlingen oefenen met het berekenen van de oppervlakte.
Om te controleren of de leerlingen de oppervlakte van verschillende figuren kunnen berekenen, kun je de volgende vragen stellen:
- Hoe kun je een oppervlakte berekenen van verschillende soorten driehoeken?
- Hoe kun je de oppervlakte berekenen van een ruit?
- Hoe kun je de oppervlakte berekenen van een parallellogram?
Inoefening
De leerlingen oefenen met het berekenen van de oppervlakte van verschillende figuren. Eerst berekenen ze de oppervlakte van een driehoek, vervolgens van een ruit en daarna van een parallellogram.
Afsluiting
Je bespreekt met de leerlingen nog eens dat het handig is om de oppervlakte te kunnen berekenen van figuren, omdat je zo handig kunt uitrekenen hoe groot iets is. Vervolgens laat je meerdere verschillende figuren zien waarbij de leerlingen moeten uitrekenen wat de oppervlakte is. Vraag de leerlingen hoe zij bij elk figuur de oppervlakte hebben berekend.
Aandachtspunten
Wanneer leerlingen moeite hebben met het berekenen van de oppervlakte van een figuur, kun je laten zien welke formule bij welk soort figuur hoort.
Ontdek meer!
Over Gynzy
Gynzy maakt onderwijs makkelijker én leuker. Versterk je onderwijs met kant-en-klare lessen, activiteiten en hulpmiddelen. Hiermee bespaar je tijd die je weer in kunt zetten waar het er echt toe doet: voor de klas.
Gynzy geeft leerkrachten weer tijd om les te geven.



